

The Terrible Tangents
Assignment 7
By Amber Candela
________________________________________________________________________________________________________________________________________________________________
The Problem
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
To do this, you first construct a circle and then another circle within it. Create a line through the center of the larger circle. Create a circle with the center at the intersection of the line and the radius the same as the smaller circle.

After you have created the circle, then construct the midpoint between the center of the smaller circle and the the intersection of the line and the constructed circle, outside the larger circle.
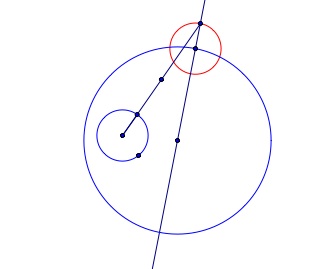
When the midpoint has been created, construct the line through the midpoint that is perpendicular to that line. The intersection of the perpendicular line and the line through the center of the circle is the center of the circle that will be tangent to both circles.
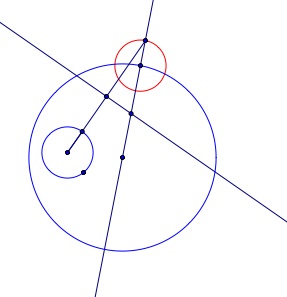
To find the radius of the tangent circle you must use the distance between the center of the circle and the center of the constructed circle. This gives you a circle that is tangent to both of the original circles.
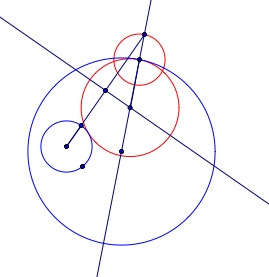
Lets clean this up! Now you can see the red tangent circle and the two blue original circles.
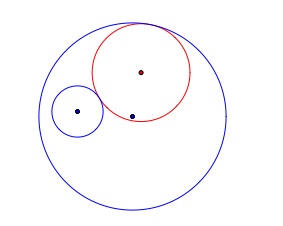
Could this tangent circle be anywhere?
If we trace the center of the tangent circle we can see the locus of points that would be the center of any circle that is tangent to both circles. The image below shows the locus of points that could be the center of a circle that is tangent to both original circles. Does the locus of points look familiar? The center of the smaller circle and the center of the large circle create the foci for the ellipse, which is also the locus of points.
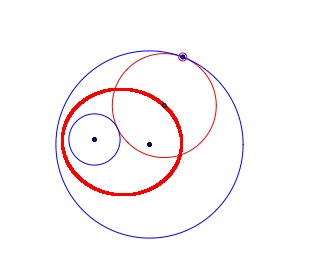
What else do you notice?
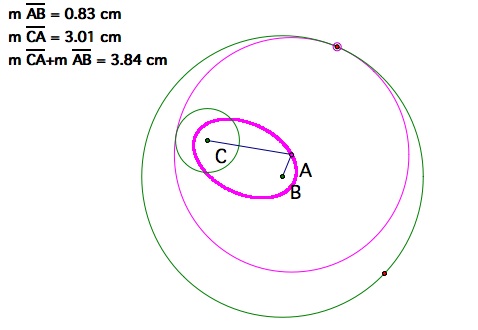
The sum of the distances from the center of the small circle to the center of the tangent circle and the center of the large circle to the center of the tangent circle will always be the same. In this case the sum will be 4.21.

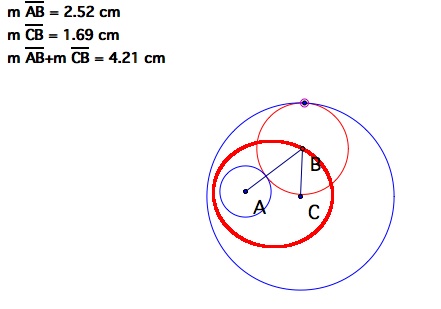
Don't believe me?
Click on the GSP file below
Is there a different tangent circle that can be drawn?
When we constructed the first tangent circle we used the intersection of the constructed circle and the line through the center of the large circle that was outside the circle. What if we used the intersection that was inside the circle? Create the segment that connects the center of the smaller circle and the intersection of the constructed circle and the line through the center of the larger circle that lies inside the larger circle.
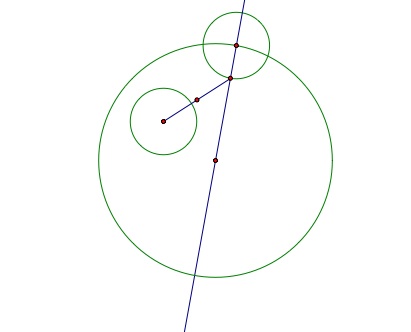
Once you have found that segment, find the midpoint and construct the perpendicular through the midpoint to that line. The intersection of the perpendicular and the line through the center of the larger circle will be the center of the tangent circle. The radius of the tangent circle will be the length from the center to the center of the constructed circle.

Lets clean this up!
There is a second circle that is tangent to both original circles.
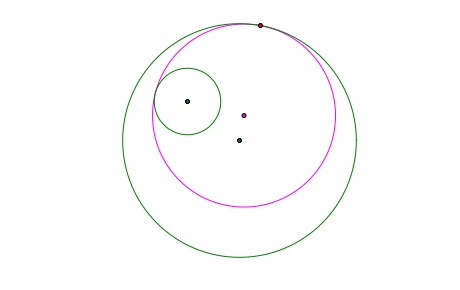
The image below shows the locus of points that is created if we look at where all the centers of the possible tangent circles are. The centers of the circles once again create the foci of the ellipse, which is the locus of points that is the collection of possible centers for the tangent circle.
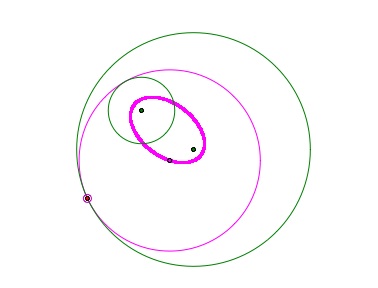
Once again the sum of the distances from the center of the small circle to the center of the tangent circle and the center of the large circle to the center of the tangent circle will always be the same.

Click the GSP document below to explore
What if we trace both tangent circles?
If we construct both tangent circles and trace them on the same graph what will happen? Two ellipses will be created with the same foci.

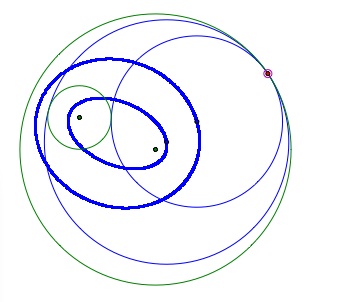
To explore both tangents, click on the link below.
Other cases
This is only the case when the one circle is inside another circle. What happens if the original circles overlap? If they are next to each other?
Overlapping Circles
Below are the two tangent circles that are created when the circles are overlapping.

Locus of points
If you trace the centers of the tangent circles, the locus of points creates an ellipse and a hyperbola with the same foci.

Below is the GSP link to explore and see the animation
Side by Side Circles
Below are the two tangent circles that are created when the circles are side by side
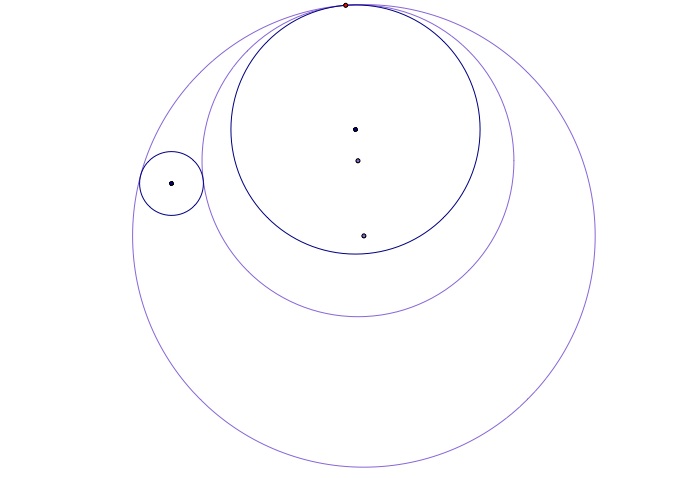
If you trace the centers of the tangent circles, the locus of points creates two hyperbolas with the same foci.

Use the GSP file below to explore and see the animations